Công thức tính chu vi hình tam giác chi tiết và dễ hiểu nhất
Bên cạnh các hình như hình chữ nhật, hình bình hành hay hình tam giác cũng là một trong những kiến thức toán học vô cùng quan trọng và được giảng dạy xuyên suốt trong quá trình học tập của học sinh. Vậy hình tam là giác là gì ? Chu vi hình tam giác tính ra ra sao. Hãy cùng chúng tôi ôn lại những kiến thức đơn giản này qua bài viết dưới đây.
Hình tam giác là gì? Tính chất của hình tam giác ?
Hình tam giác là một loại hình khá cơ bản trong toán học đây là hình hai chiều phẳng có 3 đỉnh và 3 điểm không thẳng hàng và 3 cạnh là 3 đoạn thẳng nối các đỉnh với nhau. Bên cạnh đó, tam giác còn là đa giác có số cạnh ít nhất là 3 cạnh. Ngoài ra, tam giác luôn có một đa giác đơn và một đa giác lồi các góc trong luôn nhỏ hơn 180 độ.
Ký hiệu của tam giác thường có các cạnh là AB, BC,AC
Phân loại tam giác
Để phân loại tam giác người ta chia thành 4 loại chính bao gồm:
- Tam giác cân: Là tam giác có hai cạnh bên bằng nhau
- Tam giác đều: Là tam giác có ba cạnh đều bằng nhau
- Tam giác vuông: Là tam giác có một góc vuông bằng 90 độ
- Tam giác vuông cân: Là tam giác có hai cạnh góc vuông bằng nhau
Tính chất của tam giác
- Trong một tam giác, tổng ba góc bằng 180 độ.
- Hiệu độ dài của 2 cạnh tam giác sẽ nhỏ hơn độ dài mỗi cạnh và nhỏ hơn tổng độ dài 2 cạnh.
- Cạnh lớn hơn trong một tam giác sẽ là cạnh đối diện với góc lớn nhất.
- Trực tâm của tam giác chính là điểm giao nhau của ba đường cao trong tam giác.
- Trọng tâm của tam giác là điểm giao nhau của ba đường trung tuyến.
- Đường trung tuyến là đường thẳng phân chia tam giác thành 2 phần bằng nhau về diện tích.
- Tâm của đường tròn ngoại tiếp tam giác chính là điểm giao nhau của ba đường trung trực tam giác.
- Tâm của đường tròn nội tiếp tam giác chính là điểm giao nhau của ba đường phân giác trong tam giác
Công thức tính chu vi hình tam giác
Để tính chu vi tam giác một cách dễ dàng và đơn giản nhất chúng tôi sẽ giới thiệu đến bạn một số công thức tính nhanh.
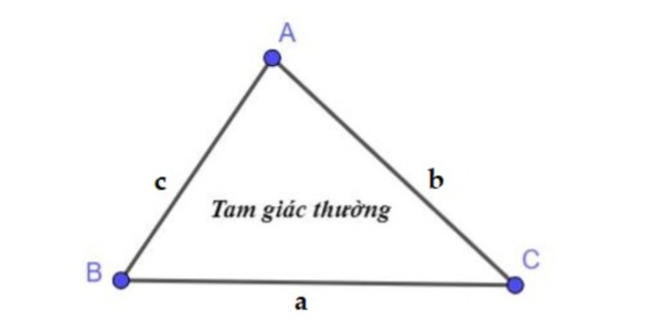
Công thức tính chu vi tam giác thường
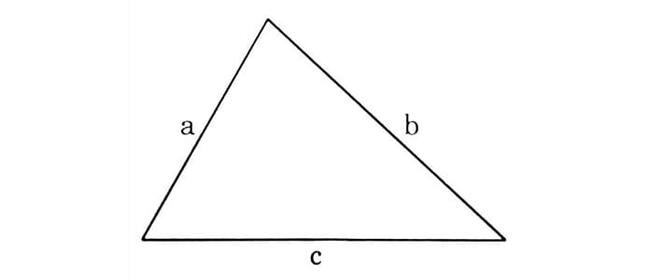
Tam giác thường là loại tam giác cơ bản nhất, có độ dài các cạnh và số đo các góc trong cũng khác nhau.
Ta có công thức như sau: P = a + b + c
Trong đó:
P: là chu vi của tam giác
a,b,c: là độ dài của 3 cạnh
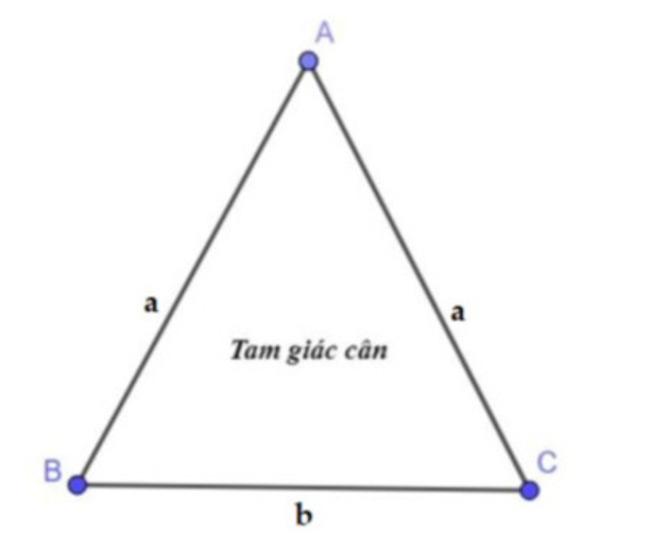
Công thức tính chu vi tam giác cân
Tam giác cân là tam giác có hai cạnh, hai góc bằng nhau và đỉnh của nó là giao điểm của hai cạnh bên.
Chu vi của tam giác cân bằng hai lần của cạnh bên cộng với cạnh đáy của hình.
Ta có công thức: P = 2a + c
Trong đó:
a: là độ dài cạnh bên của tam giác cân
c: là độ dài cạnh đáy của tam giác
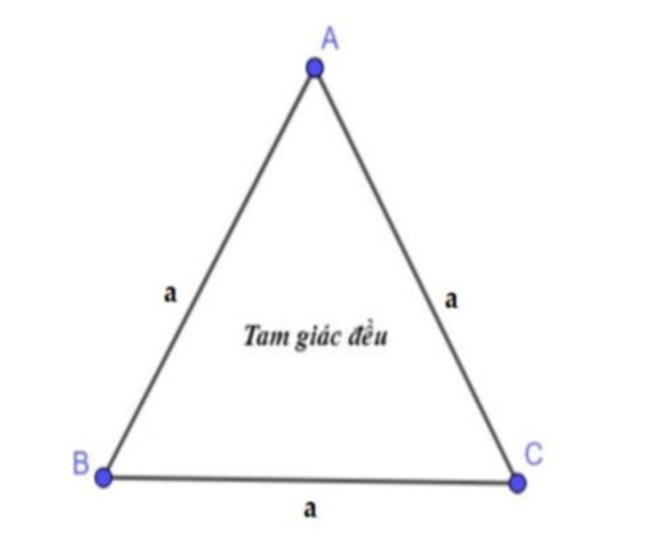
Công thức tính chu vi tam giác đều
Tam giác đều là tam giác có ba cạnh, ba góc nhọn bằng nhau và đây là trường hợp đặc biệt của tam giác cân.
Chu vi tam giác đều bằng tổng độ dài của ba cạnh và ba cạnh của tam giác bằng nhau nên bằng độ dài của một cạnh nhân với ba.
Ta có công thức tính nhanh như sau: P = a + a + a = 3a
Trong đó:
a: là độ dài các cạnh của tam giác nói trên
Công thức tính chu vi tam giác vuông
Tam giác vuông là tam giác có một góc vuông bằng 90 độ
Chu vi tam giác vuông được tính bằng tổng chiều dài ba cạnh của tam giác
Công thức tính: P = a + b + c
Trong đó:
a, b: là độ dài hai cạnh của tam giác vuông
c: là độ dài cạnh huyền của tam giác vuông
Hướng dẫn cách tính chu vi hình Tam giác
Để tính chu vi tam giác chính xác và dễ dàng nhất dưới đây chúng tôi sẽ hướng dẫn đến bạn cách tính siêu đơn giản.
Cách tính chu vi khi biết chiều dài 3 cạnh của 1 tam giác
Bước 1: Ghi nhớ lại công thức tính tính chu vi của một tam giác
Chu vi của một tam giác là tổng chiều dài ba cạnh của tam giác đó
Ví dụ: Tam giác có ba cạnh a, b, c và chu vi P được xác định như sau: P = a + b + c
Bước 2: Xác định chiều dài ba cạnh của tam giác có độ dài bằng nhau. Chính vì vậy mà bạn cần phải nhớ công thức tính chu vi tam giác đều của nó.
Ví dụ: Chiều dài ba cạnh của tam giác lần lượt là a = 3cm, b = 3cm, c = 3cm
Bước 3: Cộng chiều dài ba cạnh để tìm chu vi
Ví dụ: Cho ba cạnh của tam giác lần lượt là a = 4, b =5, c = 6. Vậy chu vi của tam giác có công thức là: P = 4 + 5 + 6 = 15
Bước 4: Sau cùng là ghi đơn vị vào sau đáp án thường đơn vị là cm hoặc m
Cách tính chu vi của tam giác vuông khi biết 2 cạnh của nó
Bước 1: Ghi nhớ lại công thức tính chu vi của tam giác
Tam giác vuông là tam giác có một cạnh góc vuông bằng 90 độ và cạnh đối diện của góc vuông đó luôn là cạnh dài nhất trong ba cạnh.
Công thức tính chu vi của tam giác vuông: P = a + b + c
Bước 2: Tiếp theo nhớ lại định lý Py ta go
Công thức tính: a2 + b2 = c2
Bước 3: Nên đặt tên cho các cạnh lần lượt a, b và c trong tam giác
Cạnh dài nhất của tam giác vuông là cạnh huyền nó nằm đối diện với hai cạnh góc vuông
Bước 4: Nhập chiều dài mà bạn đã biết vào định lý Py ta go
Ví dụ : a = 3, b = 2 => Áp dụng định lý py ta ta có: 32 + 22 = 13
Bước 5: Tìm phương trình và tìm độ dài cạnh còn thiếu
- Để tính độ dài ba cạnh cần biết tính bình phương của chúng.
- Nếu bạn đang cần tìm cạnh huyền thì cộng hai cạnh đó với nhau sau đó căn bậc hai của kết quá đó là tìm được.
- Ngược lại nếu muốn tìm độ dài cạnh kề góc vuông bạn phải thực hiện phép trừ sau đó căn bậc 2 của giá trị đó lên là sẽ tìm được cạnh cần tim.
Bước 6: Cuối cùng là cộng chiều dài của ba cạnh để tìm chu vi
Chu vi của tam giác sẽ có công thức: P = a + b + c, sau khi đã tìm được các cạnh của tam giác đó bạn chỉ cần cộng chúng lại với nhau sẽ tìm được kết quả
Ví dụ: P = 3 + 5 + 6 = 14
Cách tính chu vi của tam giác cạnh – góc – cạnh bằng định lý Cosin
Bước 1: Cần phải nắm chắc kiến thức của định lý Cos
Định lý Cos giúp bạn giải khi biết chiều dài hai cạnh và số đo góc xen giữa hai cạnh đó.
Công thức: c2 = a2 + b2 – 2ab cos(C).
Bước 2: Gắn các chữ cái đại diện cho thành phần của nó
Đầu tiên bạn viết cạnh là a và góc đối diện A. Tiếp theo cạnh thứ 2 là b và góc đối diện B và cuối cùng góc cuối là C.
Ví dụ: Cho tam giác với 2 cạnh lần lượt là 6, 8 và góc nằm giữa chúng có số đo là 86°.
Bước 3: Thay thông tin vào phương trình rồi tìm cạnh c
Bạn nên tìm bình phương cạnh a và b sau đó rồi cộng chúng lại với nhau. Sau đó tìm cosin của góc C bằng cách sử dụng máy tính cầm tay.
Bước 4: Cuối cùng là tìm chiều dài c để tính chu vi của tam giác
Công thức tính chu vi ta có công thức: P = a + b + c
Bạn chỉ cần cộng chiều dài cho cạnh vừa tính được cho cạnh c với các giá trị đã có a và b
Một số bài tập tính chu vi tam giác
Bài tập tính có lời giải chi tiết
Bài 1: Tính chu vi hình tam giác có độ dài các cạnh là 6 cm, 8cm, 20 cm.
Lời giải:
Chu vi của tam giác là: 6 + 8 + 20 = 34 (cm)
Đáp số: 34cm
Bài 2: Cho độ dài các cạnh của hình tam giác là a, b, c
Gọi P là chu vi của hình tam giác. Viết công thức tính chu vi P của hình tam giác đó.
- b) Tính chu vi của hình tam giác biết:
- a = 3cm, b = 2 cm và c = 1 cm;
- a = 5 cm, b = 5 cm và c = 3 cm;
- a = 8 dm, b = 8 dm và c = 8 dm.
Lời giải
- Công thức tính chu vi tam giác là: P = a + b + c
- Nếu a = 3cm, b = 2 cm và c = 1 cm thì ta có công thức P = 3 + 2 + 1 = 6 cm
Nếu a = 5 cm, b = 5 cm và c = 3 cm thì ta có công thức P = 5 +5 + 3 = 13 cm
Nếu a = 8 dm, b = 8 dm và c = 8 dm thì ta có công thức P = 8 +8 +8 = 24 cm
Bài 3: Tính chu vi hình tam giác có độ dài các cạnh là:
- a) 4cm, 6cm, 12cm.
- b) 20dm, 30dm,10dm.
- c) 20cm, 25cm, 40cm.
Lời giải
- a) Chu vi hình tam giác có độ dài các cạnh như trên là: 4 + 6 + 12 = 22 (cm). Đáp số: 22cm.
- b) Chu vi hình tam giác có độ dài các cạnh như trên là: 20 + 30 + 10 = 60 (dm). Đáp số: 60dm.
- c) Chu vi hình tam giác có độ dài các cạnh như trên là: 20 + 25 + 40 = 85 (cm). Đáp số: 85cm
Bài tập tự luyện
Câu 1: Hình tam giác BCD có cạnh BC dài 6cm, cạnh CD dài 12cm, cạnh DB dài 16cm. Tính chu vi hình tam giác BCD.
Câu 2: Tính chu vi hình tam giác ABC có độ dài các cạnh lần lượt là: 6dm, 15cm, 2dm 5cm.
Câu 3: Tính chu vi hình tam giác ABC biết: cạnh AD dài 9cm, chu vi hình tam giác ACD là 30cm, chu vi hình tam giác ADB là 64cm
Câu 4: Tính chu vi hình tam giác ABC, giác ABC có 6 cạnh bằng nhau và bằng 9
Câu 5: Cho tam giác BCD có độ dài cạnh BC bằng 17 cm. Tổng độ dài hai canh CD và DB hơn độ dài cạnh BClà 9cm.
a) Tìm tổng độ dài hai cạnh CD và DB
b) Tìm chu vi tam giác BCD.
Câu 6: Tính chu vi hình tam giác có độ dài ba cạnh lần lượt là:
a) 8cm, 12cm và 14cm
b) 5dm, 3dm và 5dm
c) 7m, 10m và 5m
Câu 7: Tam giác có ba cạnh bằng nhau và bằng 8dm. Tính chu vi của tam giác đó
Trên đây là công thức tính chu vi hình tam giác chi tiết và dễ hiểu nhất mà đội ngũ nhân viên Phongreviews chúng tôi đã tổng hợp. Hy vọng những thông tin mà chúng tôi chia sẻ trên hữu ích đối với bạn. Nếu có bất kỳ thắc mắc hay câu hỏi nào thì có thể bình luận phía dưới chúng tôi sẽ giải đáp và hỗ trợ.