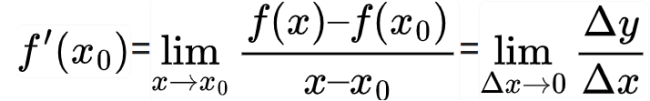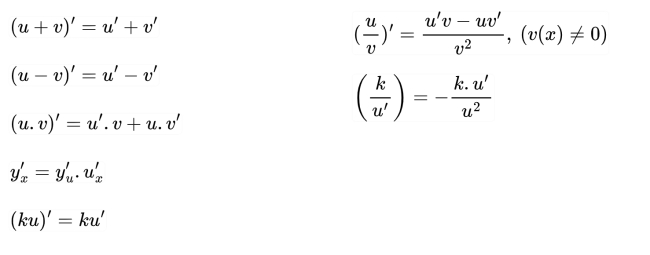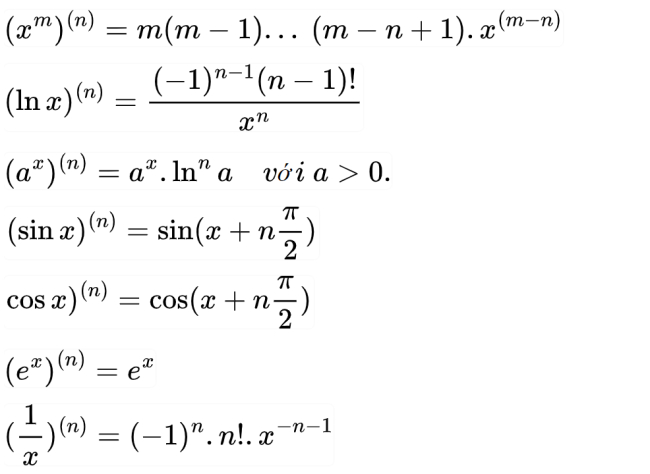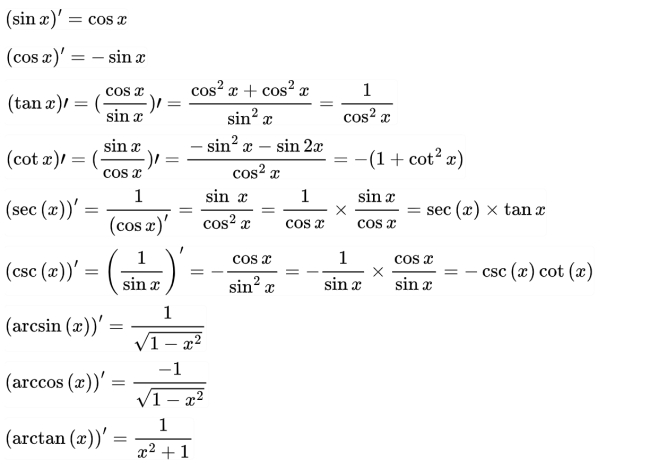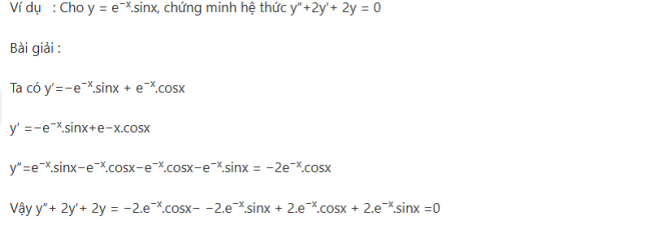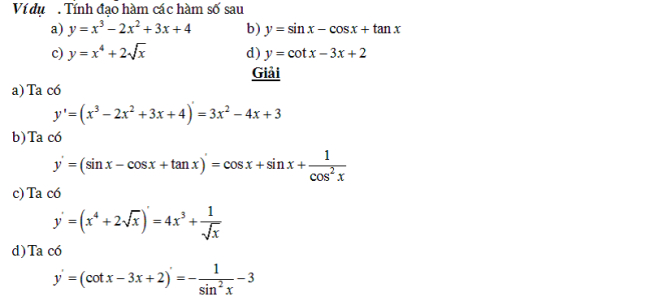Mai Anh
Công thức đạo hàm và đạo hàm lượng giác là một trong những kiến thức quan trọng nhưng cũng không kém phần phức tạp. Để giải nhanh và chính xác, học sinh phải thuộc lòng các công thức đạo hàm thường gặp. Dưới đây là tổng hợp các công thức đạo hàm của hàm số lượng giác và bài tập minh họa có lời giải chi tiết do Phongreview tổng hợp và chia sẻ với các bạn.
Đạo hàm là gì? Định nghĩa về đạo hàm
Trong phân tích toán học, đạo hàm là một hàm mô tả sự biến thiên tại một điểm. Nói cách khác, đạo hàm là tỷ số giữa số gia và hàm số tại một điểm x0. Độ lớn của biến thiên và chiều của biến thiên thể hiện giá trị của đạo hàm.
Tuy nhiên, theo một định nghĩa khác của Wikipedia, đạo hàm được hiểu là biến thiên lên và xuống của hàm số ở điểm biến thiên . Cũng trong vật lý, đạo hàm được coi là vận tốc tức thời khi một vật đang chuyển động.
Đạo hàm của hàm số y=f(x) được ký hiệu bằng y′(x0) hoặc f′(x0):
Trong đó:
- Số gia của đối số là Δx=x−x0
- Số gia của hàm số là Δy=y−y0
Tham khảo: Công thức 7 Hằng đẳng thức đáng nhớ đầy đủ, chính xác nhất
Bảng công thức đạo hàm và đạo hàm lượng giác
Công thức đạo hàm của tổng, hiệu, tích, thương
Giả sử u= u(x) và v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
Đạo hàm các hàm số sơ cấp và đạo hàm của hàm hợp
Đạo hàm cấp cao
Quy tắc đạo hàm của hàm số hợp
Nếu y = y(u(x)) thì y'(x) = y'(u)Xu'(x)
Công thức đạo hàm lượng giác
Bảng công thức đạo hàm đầy đủ
Các dạng bài toán liên quan đến công thức đạo hàm
Dưới đây là tổng hợp một số dạng toán và bài tập có ví dụ minh họa để các bạn dễ hiểu và nắm vững hơn bằng cách áp dụng các công thức đạo hàm:
Dạng 1: Áp dụng định nghĩa tính đạo hàm
Đây là một trong những dạng toán cơ bản về đạo hàm, với cách giải phương trình đơn giản nhất. Để giải bài tập, học sinh vận dụng theo định nghĩa và sử dụng các công thức cơ bản để tính chính xác nhất. Cụ thể:
Dạng 2: Chứng minh hệ thức
Dạng toán này tập trung vào việc chứng minh một hệ thức dựa trên một điều kiện hiện có. Bạn phải cố gắng tính toán chính xác nhất có thể để có được kết quả cuối cùng.
Dạng 3: Biết tiếp điểm, viết phương trình tiếp tuyến
Đây là một trong những dạng giải bài tập khá phổ biến. Cụ thể là sẽ có một phương trình tiếp tuyến của hàm số trên đồ thị của đường cong (C): y= f(x) tại tiếp điểm M( x0 ; y0) và có dạng: y = y’(x0)(x-x0) + y0.
Ví dụ: Cho một hàm số y= x3 + 3mx2 + ( m+1)x + 1 (1), m là một tham số thực. Hãy tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số tại điểm có hoành độ x = -1 và đi qua điểm A( 1;3).
TXD: D = R
y’ = f'(x)= 3×2 + 6mx + m + 1
Với x0 = -1 => y0= 2m -1, f'( -1) = -5m + 4
Phương trình tiếp tuyến tại M( -1; 2m – 1) : y= ( -5m + 4 ) ( x+1) + 2m -1 (d)
Ta có A ( 1;3) ∈ (d) <=> ( -5m + 4).2 + 2m – 1 = 3 => m = 1/2
Dạng 4: Viết phương trình tiếp khi biết hệ số góc
Hãy viết phương trình tiếp tuyến Δ của ( C ) : y = f( x ), khi biết Δ có hệ số góc là k cho trước
Gọi M( x0 ; y0) là tiếp điểm. Tính y’ => y'(x0)
Phương trình tiếp tuyến Δ có hệ số góc k => y’ = ( x0 ) = k (i)
- x0 => y0 = f(x0) => Δ : y = k (x – x0 )+ y0
Lưu ý: Hệ số góc k = y'( x0 ) của tiếp tuyến Δ thường cho kiểu gián tiếp như sau:
Ví dụ: Cho hàm số y=x3+3×2-9x+5 ( C). Tìm tiếp tuyến có hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của đồ thị ( C ).
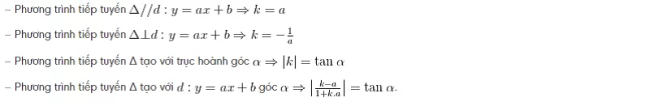
Ta có y’ = f'( x ) = 3×2 + 6x – 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x0) = 3 x02 + 6 x0 – 9
Ta có 3 x02 + 6×0– 9 =3 ( x02+ 2×0 +1) – 12 = 3 (x0+1)2– 12 > – 12
Vậy min f( x0)= – 12 tại x0= -1 => y0=16
Suy ra phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4
Dạng 5: Bất phương trình và phương trình có đạo hàm
Dạng toán này sẽ kết hợp với nhiều công thức để có thể giải phương trình hoặc một bất phương trình được đưa ra để tính toán ra được kết quả cuối cùng.
Dạng 6: Dùng công thức tính đạo hàm
Ở đây, bạn cần biết các công thức đạo hàm cơ bản để có thể giải các bài toán một cách chính xác. Nếu rơi vào tình huống gặp phải các hàm phức tạp, bạn có thể đơn giản hàm đó bằng cách rút gọn trước rồi mới tiến hành tính đạo hàm, đặc biệt là đối với các hàm lượng giác.
Dạng 7: Phương trình tiếp tuyến tại một điểm cho trước thuộc đồ thị/có hệ số góc cho trước của đồ thị hàm số
Các bạn học sinh cần phải nắm vững được hai dạng viết phương trình tiếp tuyến cơ bản như sau đây:
Dạng 8: Tính đạo hàm cấp cao
Đạo hàm cấp cao các dạng bài tập thường thiên về tính đạo hàm cấp 2 trở lên, khi đó các bạn có thể áp dụng công thức y(n) = (y(n-1))’.
Còn đối với trường hợp để tính đạo hàm cấp n, các bạn sẽ phải tính đạo hàm từ cấp 1, 2, 3,…. rồi từ đó mới tìm ra được công thức tính đạo hàm cấp n. Thường có thể áp dụng vào phương pháp quy nạp toán học để có thể chứng minh được công thức đó là đúng.
Trên đây là những kiến thức hữu ích về các công thức đạo hàm thông dụng nhất. Hi vọng qua bài viết bạn đã hiểu rõ về công thức đạo hàm và ứng dụng của nó trong thực tế. Từ đó áp dụng để giải bài tập để đạt kết quả tốt.
