Trực tâm là gì? Tính chất của trực tâm trong tam giác đơn giản và dễ hiểu
Trực tâm trong tam giác là một kiến thức Toán quan trọng đối với học sinh và được ứng dụng nhiều và các bài kiểm tra thường ngày. Vậy trực tâm của tam giác là? Tính chất của trực tâm trong tam giác được tính ra sao? Hãy cùng chúng tôi tìm hiểu trong bài viết dưới đây.
Trực tâm là gì? Dấu hiệu nhận biết
Trực tâm là giao điểm của 3 đường cao tương ứng của 3 đỉnh trong một tam giác. Mỗi tam giác bất kì thì chỉ có một trực tâm duy nhất mà thôi. Trực tâm có thể nằm trong hoặc ngoài của tam giác đó.
Tính chất: Khoảng cách từ một đỉnh tới trực tâm của một tam giác bằng hai lần khoảng cách từ tâm của đường tròn ngoại tiếp tam giác đó đến trung điểm của cạnh nối hai đỉnh còn lại.
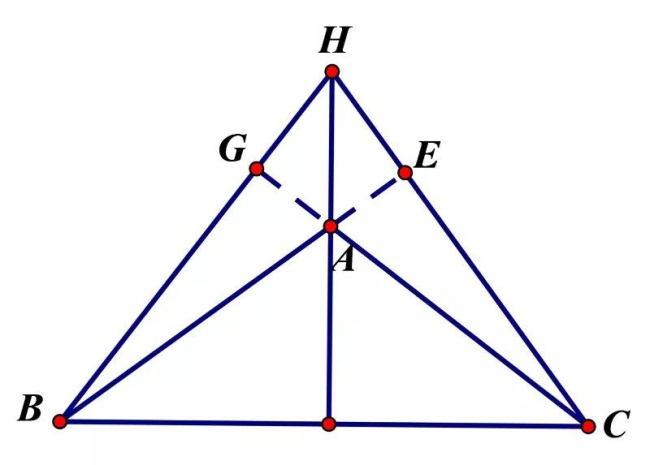
- Đối với tam giác nhọn: Trực tâm nằm ở miền trong tam giác đó.
- Đối với tam giác vuông: Trực tâm chình là đỉnh góc vuông.
- Đối với tam giác tù: Trực tâm nằm ở miền ngoài tam giác đó.
- Tham khảo thêm: Công thức tính chu vi hình tam giác chi tiết và dễ hiểu nhất
Khái niệm đường cao của một tam giác
Đường cao của tam giác là đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện, độ dài của đường cao là khoảng cách giữa đỉnh và đáy, theo đó mỗi tam giác sẽ có ba đường cao.
Tính chất của trực tâm của tam giác
Tính chất trực tâm của tam giác bao gồm những tính chất sau:
- Trong một tam giác cân, đường trung trực ứng với cạnh đáy cũng chính là đường phân giác, đường trung tuyến và đường cao của tam giác đó.
- Trong 1 tam giác, nếu như có một đường trung tuyến đồng thời là phân giác thì tam giác đó là tam giác cân.
- Trong 1 tam giác, nếu như có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác cân.
- Trực tâm của tam giác nhọn ABC sẽ trùng với tâm đường tròn nội tiếp tam giác tạo bởi 3 đỉnh là chân ba đường cao từ các đỉnh A, B, C đến các cạnh BC, AC, AB tương ứng.
- Đường cao tam giác ứng với 1 đỉnh cắt đường tròn ngoại tiếp tại điểm thứ 2 sẽ là đối xứng của trực tâm qua cạnh tương ứng.
Cách xác định trực tâm ở trong tam giác
Xác định trực tâm của tam giác bằng hai đường cao theo đó thì đối với tam giác tù, tam giác nhọn hoặc tam giác cân, tam giác đều thì cách xác định trực tâm là giống nhau là xong.
Cách xác định: Từ hai đỉnh của tam giác, bạn kẻ đường cao tương ứng đến 2 cạnh đối diện. Khi đó, trực tâm của tam giác chính là điểm giao nhau của 2 đường cao đó và chắc chắn đường cao còn lại cũng đi qua điểm này mặc dù không cần kẻ.
- Tham khảo thêm: Công thức tính chu vi hình chữ nhật nhanh và chính xác nhất
Cách chứng minh trực tâm của tam giác
Trực tâm của tam giác vuông
Trực tâm của tam giác vuông chính là đỉnh của góc vuông.
Ví dụ: Tam giác vuông MNP có trực tâm H trùng với góc vuông N.
Trực tâm của tam giác nhọn
Tam giác nhọn ABC có trực tâm H nằm ở miền trong tam giác.
Trực tâm của tam giác tù
Trực tâm của tam giác tù nằm ở miền ngoài tam giác đó.
Ví dụ: Tam giác tù ABC có trực tâm H nằm ở miền ngoài tam giác đó.
Một số bài tập về trực tâm
Bài tập trực tâm có lời giải
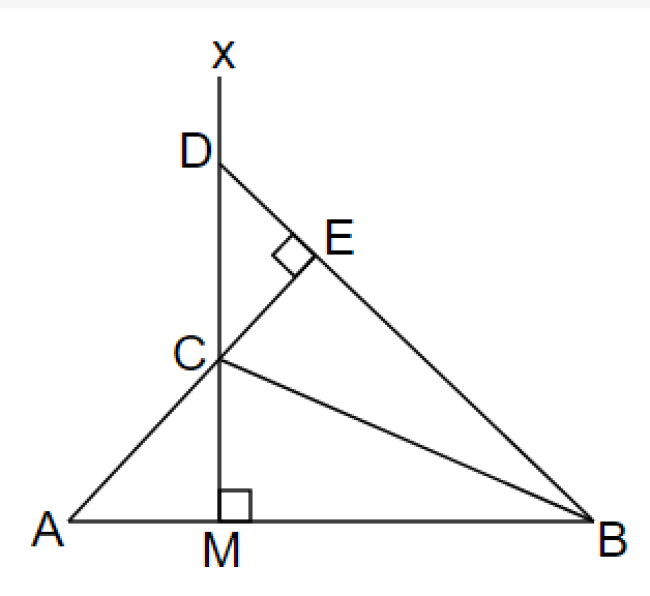
Câu 1: Cho đoạn thẳng AB có M nằm giữa A và B (MA<MB). Kẻ Mx vuông góc với AB. Trên Mx lấy 2 điểm C và D sao cho MA=MC, MB=MD. Tia AC cắt BD tại E. Chứng minh:
a. AE vuông góc với BD
b. D là trực tâm của ∆ABC
Giải
a.Ta có Mx vuông góc với AB, C ∈ Mx, MC = MA,
Suy ra tam giác BMD vuông cân tại M => Có góc MAC = góc MCA bằng 45 độ
=> góc MAC = góc MDB = 45 độ. Hay góc MAC = góc CDE = 45 độ
Suy ra tam giác CED vuông cân tại E => AE vuông góc với BD điều phải chứng minh.
b. Ta có BD vuông góc với AC tại E, MD vuông góc với AB
Suy ra D là trực tâm của tam giác ABC
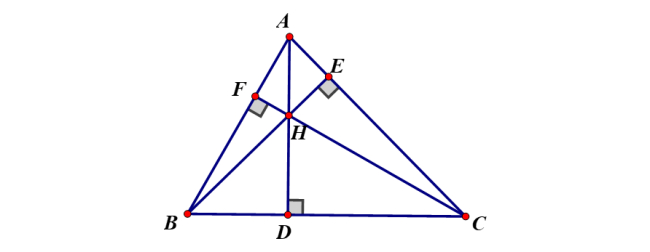
Câu 2: Cho tam giác ABC không vuông. Gọi H là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác HBC. Từ đó hãy chỉ ra trực tâm của tam giác đó.
Lời giải
Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
ΔHBC có :
AD ⊥ BC nên AD là đường cao từ H đến BC.
BA ⊥ HC tại F nên BA là đường cao từ B đến HC
CA ⊥ BH tại E nên CA là đường cao từ C đến HB.
AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB
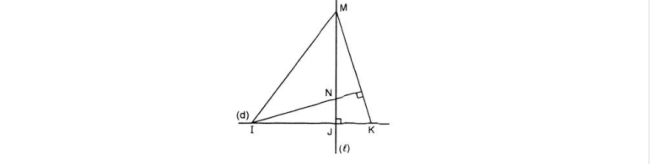
Câu 3: Trên đường thẳng d, lấy ba điểm phân biệt I, J, K (J ở giữa I và K).
Kẻ đường thẳng l vuông góc với d tại J. Trên l lấy điểm M khác với điểm J. Đường thẳng qua I vuông góc với MK cắt l tại N.
Chứng minh KN ⊥ IM.
Lời giải
l ⊥ d tại J, và M, J ∈ l ⇒ MJ ⟘ IK ⇒ MJ là đường cao của ΔMKI.
N nằm trên đường thẳng qua I và vuông góc với MK ⇒ IN ⟘ MK ⇒ IN là đường cao của ΔMKI.
IN và MJ cắt nhau tại N .
Theo tính chất ba đường cao của ta giác ⇒ N là trực tâm của ΔMKI.
⇒ KN cũng là đường cao của ΔMKI ⇒ KN ⟘ MI.
Vậy KN ⏊ IM
Bài tập tự luyện
Câu 1: Cho tam giác MNP với trực tâm H. Chứng minh rằng các điểm đối xứng với H qua các đường thẳng chứa các cạnh hay trung điểm của các cạnh nằm trên đường tròn (MNP).
Câu 2: Cho tam giác ABC với các đường cao AD, BE, CF. Trực tâm H.DF cắt BH tại M, DE cắt CH tại N. Chứng minh đường thẳng đi qua A và vuông góc với MN đi qua tâm ngoại tiếp của tam giác HBC.
Câu 3: Cho G và G’ lần lượt là trọng tâm của hai tam giác ABC và A’B’C’. Chứng minh rằng véc tơ : AA’ + BB’ + CC’ = 3GG’.
Câu 4: Cho tam giác EHP không vuông. Gọi I là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác EHP. Từ đó hãy chỉ ta trực tâm của tam giác đó.
Câu 5: Cho đường tròn (O, R) , gọi KL là dây cung cố định của đường tròn và I là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác IKL.
Câu 6: Cho △ABC có các đường cao AD;BE;CF cắt nhau tại H. I; J lần lượt là trung điểm của AH và BC.
a. Chứng minh: IJ⊥EF
b. Chứng minh: IE⊥JE
Câu 7: Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.
Câu 8: Cho đường tròn (O, R) , gọi BC là dây cung cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.
Câu 9: Cho tam giác NCK với trực tâm H. Chứng minh rằng các điểm đối xứng với H qua các đường thẳng chứa các cạnh hay trung điểm của các cạnh nằm trên đường tròn (NCK).
Câu 10: Cho tam giác NLP không vuông. Gọi I là trực tâm của nó. Hãy chỉ ra các đường cao của tam giác NLP. Từ đó hãy chỉ ta trực tâm của tam giác đó.
Trên đây là một số chi tiết về bài toán trực tâm trong tam giác mà được đội ngũ Phongreviews chúng tôi đã tổng hợp được. Hy vọng những thông tin mà chúng tôi chia sẻ hữu ích đối với bạn trong vận dụng làm bài tập. Nếu có thắc mắc bạn có thể bình luận phía dưới bài viết để được giải đáp.
- Tham khảo thêm: Công thức tính diện tích hình bình hành đơn giản nhất 2023