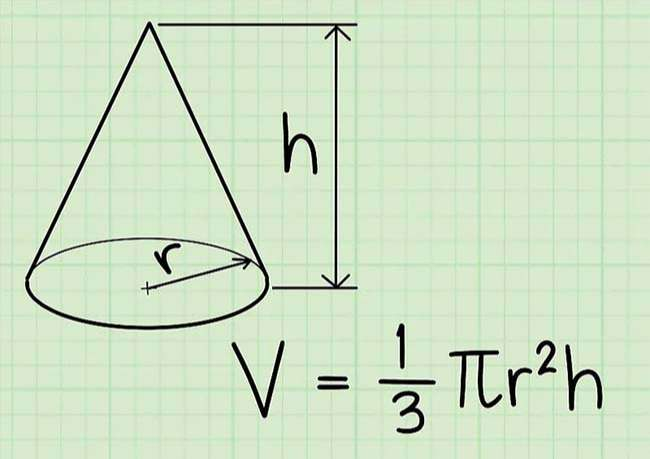Công thức tính thể tích hình nón nhanh và chính xác nhất
Thể tích hình nón là một kiến thức toán học của khối 12 được rất nhiều người xem trọng. Bởi phần lớn kiến thức này được xuất hiện rất nhiều trong các bài thi và bài kiểm tra dành cho học sinh. Vậy cách tính của công thức thể tích hình nón ra sao? Hãy cùng chúng tôi tìm hiểu trong bài viết dưới đây.
Định nghĩa về hình nón
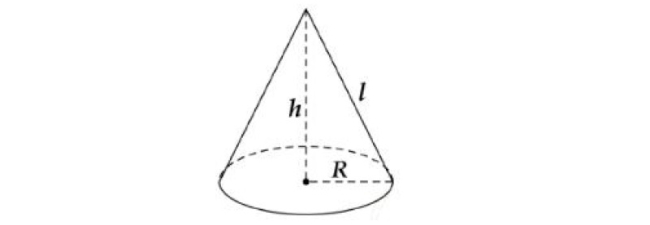
Hình nón là hình được tạo ra khi quay tam giác vuông một vòng quay cố định, đây là một khối hình học không gian 3 chiều có mặt đáy là hình tròn và một đầu nhọn có đỉnh duy nhất nằm hướng lên phía trên. Vì vậy, hình nón được ứng dụng rất nhiều trong các đồ vật cuộc sống xung quanh như: Cây kem, mũ sinh nhật hay như chiếc nón thường ngày trong gia đình chúng ta.
Các loại hình nón
Hình nón được người ta phân thành 3 loại chính:
- Hình nón cụt: Là hình có hai hình tròn nằm song song với nhau và không có đỉnh.
- Hình nón tròn: Là hình mà đỉnh được nối vuông góc với mặt phẳng đáy của tâm hình tròn đó.
- Hình nón xiên: Là hình có đỉnh không kéo vuông góc với tâm của hình tròn, mà chúng có thể kéo từ một điểm bất kỳ đến tâm của đường tròn mặt đáy.
Các thuộc tính của hình nón
Hình nón có các thuộc tính sau đây:
- Là hình không có cạnh.
- Có một đỉnh là hình của tam giác.
- Có một đường tròn được gọi là mặt đáy.
- Tham khảo thêm: Công thức tính diện tích hình lập phương đơn giản và dễ hiểu
Công thức tính thể tích hình nón
Công thức tính thể tích hình nón: V = ⅓π x r2 x h
Trong đó:
- V: Ký hiệu thể tích hình nón
- π: Hằng số pi = 3,14
- r: Bán kính hình tròn đáy của hình nón
- h: Chiều cao hạ từ đỉnh xuống tâm đường tròn đáy.
Hướng dẫn cách tính thể tích hình nón
Bước 1: Bước đầu, tìm bán kính
Trong bài nếu cho sẵn bán kinhs thì bạn có thể chuyển sang các bước tiếp theo. Còn nếu đề bài chưa cho biết bán kính thì bạn cần phải tính như sau.
- Trường hợp 1: Có đường kính -> chia 2 để ra bán kính
- Trường hợp 2: Có chu vi -> chia cho 2π để ra bán kính
- Trường hợp 3: Chưa cho dữ liệu -> dùng thước đo khoảng cách lớn nhất giữa 2 điểm trên đường tròn đáy (đường kính) và chia cho 2
Bước 2: Sử dụng bán kính vừa có được để tính diện tích đáy
Tiếp đến bạn dùng số đo bán kính vừa có và áp dụng vào công thức A = π.r2 để tính diện tích hình tròn.
Ví dụ: Ta có bán kính của đáy bằng 3 cm suy ra A = π. 9 = 28,26 cm
Bước 3: Tiếp theo là tìm chiều cao của hình nón
Nếu trong đề bài cho bạn sẵn số đo, thì bạn nên viết ra giấy. Còn nếu trong trường hợp mà để chưa cho thì bạn lấy thước để đo.
Ví dụ: Người ta cho bạn hình nón có chiều cao là 2 cm bạn cần lưu ý về chiều cao cũng như bán kính của nó phải có cùng đơn vị đo.
Bước 4: Nhân diện tích đáy với chiều cao
Tới bước này bận nên sử dụng diện tích hình tròn và chiều cao đã biết được phía trên sau đó đem chúng nhân lại với nhau.
Ví dụ: Diện tích đáy hình nón (3 cm2 ), chiều cao (2 cm2 ) = 3 x 2 = 6cm3.
Bước 5: Bước cuối cùng là chia kết quả
Sau khi đã tính được kết quả bạn lấy đáp án đó chia cho 3 để ra thể tích của hình nón.
Ví dụ: 6cm3/3 = 2 cm
Ngoài ra bạn nên chú ý đến đơn vị đo thể tích luôn là đơn vị lập phương. Vì đây là một phép đo trong không gian 3 chiều.
- Tham khảo thêm: Công thức tính diện tích hình thoi chính xác và đầy đủ ví dụ
Một số bài tập tính thể tích hình nón
Bài tập thể tích hình nón có lời giải
Câu 1: Cho r = 3 cm; h = 5 cm. Thể tích hình nón là bao nhiêu?
Giải:Thể tích hình nón = 1/3. diện tích đáy = 1/3.π.r2.h = 1/3.π.9. 5 = 47,1 cm3
Câu 2: Cho d = 2 dm, h = 1,25 dm. Thể tích hình nón là bao nhiêu?
Giải: Thể tích hình nón = 1/3. diện tích đáy = 1/3.π.r2.h = 1/3.π.1.1,25 = 0,41dm3
Câu 3: Cho r = 2,5 m, l = 4,75 m (Gợi ý nên áp dụng Py-ta-go trong tam giác vuông để tìm h). Hãy tính thể tích hình nón?
Giải: h2 + r2 = l2 => h = m. Sau khi tìm được h, áp dụng công thức thể tích hình nón ta được:
Thể tích hình nón = 1/3. diện tích đáy = 1/3.π.r2.h = 1/3.π.(2,25)2. = 5,0625 m3
Câu 4: Cho khối nón có độ dài đường sinh là 8 cm, bán kính hình tròn đáy bằng 2 cm. Hãy tính thể tích khối nón?
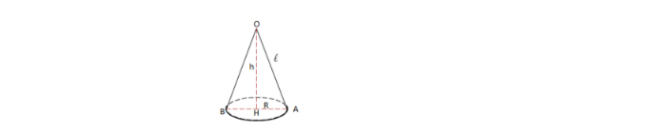
Giải: Gọi O là đỉnh khối nón, H là tâm hình tròn, A là điểm thuộc đường tròn đáy, có OA = 8cm, HA = 2cm
Trong tam giác vuông OHA, ta tính được OH: căn bậc 2 của OA2 – HA2 = căn bậc 2 của 82 – 22 = 7,74 cm
Vậy thể tích của khối nón là: V = ⅓. 7,74. 22 = 10,32 m3.
Bài tập thể tích hình nón tự luyện
Câu 1: Trong không gian, cho tam giác MNP đều cạnh bằng a. Gọi H là trung điểm của NP. Thể tích của khối nón nhận được khi quay tam giác MNP xung quanh trục MH bằng bao nhiêu?
Câu 2: Trong không gian, cho tam giác ABC vuông tại B, góc BCA = 45°, CA = 2a. Thể tích khối nón nhận được khi quay tam giác ABC xung quanh trục AC bằng bao nhiêu?
Câu 3: Cho hình nón (N) có góc ở đỉnh bằng 30°, độ dài đường sinh bằng 6. Hãy tính thể tích khối nón đã cho bằng bao nhiêu?
Câu 4: Một khối nón có thể tích bằng 14 π, nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên 3 lần thì thể tích của khối nón mới bằng bao nhiêu?
Câu 5: Cho hình nón có bán kính đáy là 6a, chiều cao là 3a. Tính đường sinh, diện tích xung quanh, diện tích toàn phần và thể tích của hình nón trên.
Câu 6: Cho hình nón có đường sinh l, góc giữa đường sinh và mặt phẳng đáy là 60º. Tính diện tích xung quanh của hình nón.
Câu 7: Cho 1 khối nón có chiều dài đường sinh là 4 cm, bán kính đáy của hình tròn là 1 cm. Áp dụng công thức để tính thể tích khối nón đã cho.
Câu 8: Cho tam giác vuông MNP vuông tại M có NP = 26cm; MN = 10cm. Quay tam giác MNP cạnh MN ta được một hình nón có thể tích là.
Câu 9: Một khối nón có thể tích bằng 45 π, nếu giữ nguyên chiều cao và tăng bán kính khối nón đó lên 3 lần thì thể tích của khối nón mới bằng bao nhiêu?
Câu 10: Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh a. Tính diện tích xung quanh của hình nón.
Cậu 11: Một hình nón có đường sinh bằng 4 cm và góc ở đỉnh bằng 60°. Cắt hình nón bởi mặt phẳng (α) đi qua đỉnh sao cho góc giữa (α) và mặt đáy bằng 40°. Tính diện tích thiết diện.
Câu 12: Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 80. Tính diện tích xung quanh của hình nón và thể tích của khối nón lần lượt là?
Câu 13: Một hình nón có đường kính đáy là a√3 , góc ở đỉnh là 140. Tính thể tích của khối nón đó theo a.
Câu 14: Một hình nón có đường sinh bằng 3a và diện tích xung quanh bằng πa2. Thể tích khối nón là.
Câu 15: Trong không gian, cho tam giác ABC vuông tại A, góc ABC = 80°, BC = 3a. Thể tích khối nón nhận được khi quay tam giác ABC xung quanh trục AC bằng.
Câu 16: Trong không gian, cho tam giác EFH đều cạnh a. Gọi I là trung điểm của FH. Thể tích của khối nón nhận được khi quay tam giác EFH xung quanh trục IE bằng.
Câu 17: Trong không gian, cho hình thang ABCD vuông tại A và D, AB = AD = a, CD = 2a. Thể tích khối tròn xoay nhận được khi quay hình thang ABCD xung quanh trục AD bằng.
Trên đây là công thức tính thể tích hình nón nhanh và chính xác nhất mà đội ngũ nhân viên Phongreviews tổng hợp và cung cấp. Hy vọng những thông tin mà chúng tôi chia sẻ trên hữu ích đối với các bạn học sinh. Nếu có thắc mắc bạn có thể bình luận phía dưới bài viết để được tư vấn giải đáp.
- Tham khảo thêm: Cách tính diện tích hình thang chi tiết, chuẩn xác nhất